根轨迹图反映了闭环特征根随\(K_r\)变化的规律,而闭环特征方程的根与系统的性能关系密切。通过根轨迹来分析系统的性能具有直观、方便的特点。
频率特性法是通过系统的开环频率特性的频域性能指标间接地表征系统瞬态响应的性能。系统性能的分析过程。
根轨迹和频率响应实验
直线一级倒立摆根轨迹控制实验
根轨迹分析
根据《倒立摆的建模仿真与控制(一)倒立摆系统的建模》中的传递函数模型,将以下实际系统参数代入:
小车质量\(M=1.096kg\)
摆杆质量\(m=0.109kg\)
小车摩擦系数\(b=0.1N\cdot s/m\)
摆杆转动轴心到杆质心的长度\(l=0.25m\)
摆杆惯量\(I=0.0034kg\cdot m^2\)
得到摆杆角度和小车加速度之间的传递函数为: \[ G(s)=\frac{\Phi(s)}{V(s)}=\frac{ml}{(I+ml^2)s^2-mgl}=\frac{0.02725}{0.0102125s^2-0.26705} \] 在MATLAB中运行以下脚本:
1 | close all; |
得到结果如下:
1 | z = |
可以看出,系统有两个零点,有两个极点,并且有一个极点为正。
绘制的系统根轨迹如下图所示:
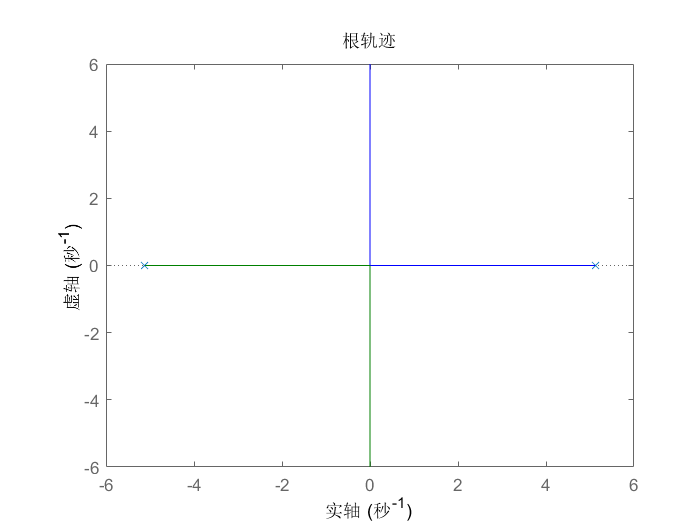
可以看出闭环传递函数的一个极点位于右半平面,并且有一条根轨迹起始于该极点,并沿着实轴向左跑到位于原点的零点处,这意味着无论增益如何变化,这条根轨迹总是位于右半平面,即系统总是不稳定的。
根轨迹校正及仿真
对于该系统,设计控制器,使得使得校正后系统的要求如下:
调整时间\(t_s=0.5s(2\%)\)
最大超调量\(M_p\le10\%\)
根轨迹设计步骤如下:
- 确定闭环期望极点\(s_d\)的位置,由最大超调量
\[ M_p=e^{-\frac{\pi\zeta}{\sqrt{1-\zeta^2}}}\times100\%\le10\% \]
解得阻尼比\(\zeta\ge0.591155\),为使系统振荡幅度小,取阻尼比\(\zeta=0.9\)。
由\(\zeta=\cos \theta\)解得\(\theta=0.4510\)。(其中\(\theta\)为位于第二象限的极点和\(O\)点的连线与实轴负方向的夹角)
又由: \[ t_s=\frac{4}{\zeta\omega_n}\le0.5 \ (2\%) \] 解得固有频率\(\omega_n\ge8.8889rad/s\),取固有频率\(\omega_n=14 \ rad/s\)。
期望闭环极点: \[ p_{1,2}=\omega_n(-\cos\theta\pm j\sin\theta)=-12.600\pm6.1025j \]
- 未校正系统的根轨迹在实轴和虚轴上,不通过闭环期望极点,因此需要引入新的零极点,对系统进行校正,使得根轨迹通过期望闭环极点,设超前校正控制器为:
\[ K(s)=\alpha\frac{Ts+1}{\alpha Ts+1}=\frac{s-z_c}{s-p_c} \ (a\le1) \]
- 计算超前校正装置应提供的相角,已知根轨迹上点满足相角方程:
\[ \angle G(s_0)+\angle K(s_0)=(2k+1)\pi \]
则有: \[ \phi_c=\angle K(s)=(2k+1)\pi-\angle G(s_0) \] 取点\(s_0=-12.600+6.1025j\),则有: \[ \begin{align} \angle G(s_0)&=-[\pi-\tan^{-1}(\frac{\omega_n\sin\theta}{\omega_n\cos\theta-5.1136})]-[\pi-\tan^{-1}(\frac{\omega_n\sin\theta}{\omega_n\cos\theta+5.1136})]\notag \\ &=-5.2675\notag \end{align} \] 则: \[ \begin{align} \phi_c&=(2k+1)\pi-\angle G(s_0)\notag \\ &=(2k+1)\pi-(-5.2061)\notag \\ &=2.1259\notag \end{align} \] 其中\(k=-1\)。
- 设计超前校正装置:
\[ \gamma=\frac12(\pi-\theta-\phi_c)=0.2823 \]
各角度示意图如下:
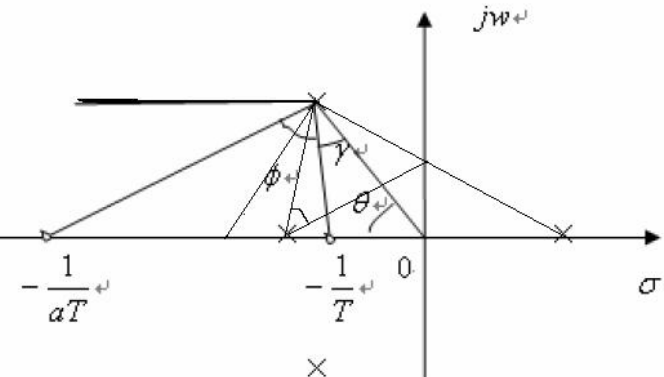
则超前校正装置零点: \[ z_c=-\frac{\omega_n\sin\gamma}{\sin(\pi-\gamma-\theta)}=-5.8268 \] 超前校正装置极点: \[ p_c=-(\omega_n\cos\theta+\omega_n\sin\theta\cot\gamma)=-33.6376 \] 校正装置的零极点相对位置如下图所示:
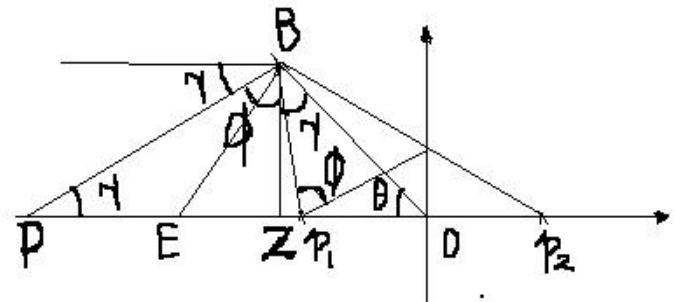
校正后开环传递函数: \[ Q(s)=G(s)K(s)=K\frac{s+5.8268}{s+33.6376}\frac{0.02725}{0.0102125s^2-0.26705} \]
- 由幅值条件\(|G(s_0)K(s_0)|=1\),并设反馈为单位负反馈,解得\(K=162.9412\)。
- 最终系统控制器为:
\[ K(s)=\frac{162.9412(s+5.8268)}{s+33.6376} \]
校正后系统根轨迹如下图所示:
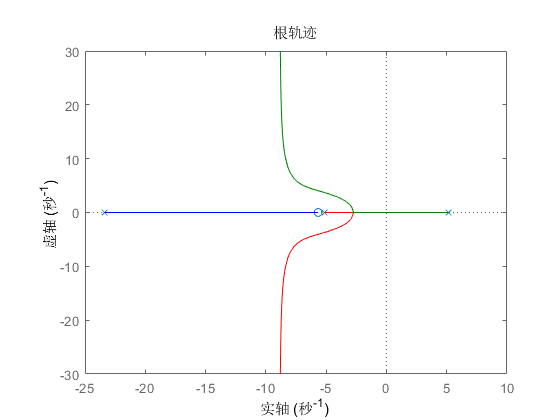
闭环系统的阶跃响应曲线如下图所示:
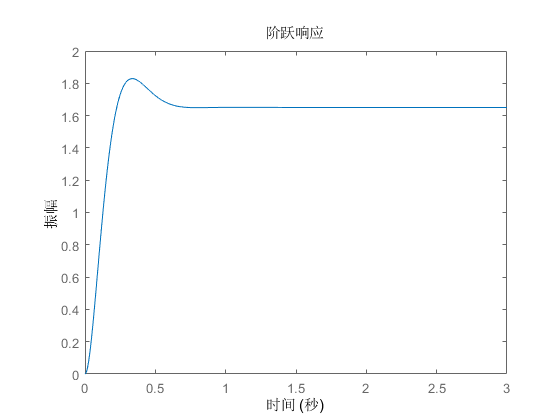
闭环系统的脉冲响应曲线如下图所示:
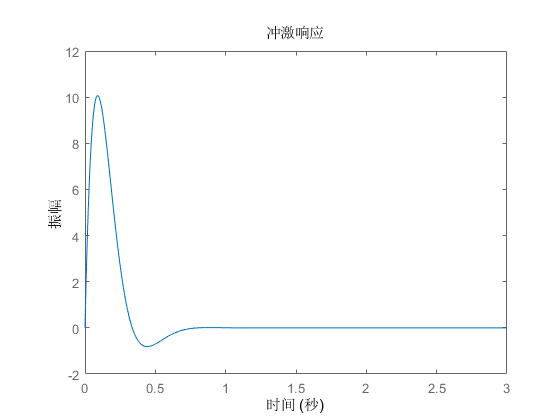
直线一级倒立摆频率响应控制实验
频率响应分析
根据《倒立摆的建模仿真与控制(一)倒立摆系统的建模》中的传递函数模型,得到摆杆角度和小车加速度之间的传递函数为: \[ G(s)=\frac{\Phi(s)}{V(s)}=\frac{0.02725}{0.0102125s^2-0.26705} \] 在\(MATLAB\)下绘制系统的\(Bode\)图和\(Nyquist\)图。
在\(MATLAB\)中运行以下脚本:
1 | num=[0.02725]; |
得到结果如下:
1 | z = |
系统的的\(Bode\)图如下:
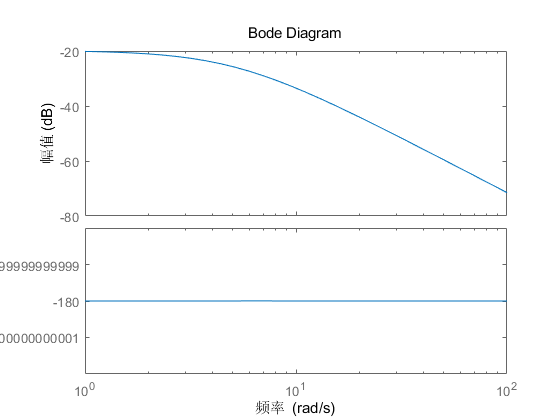
系统的的\(Nyquist\)图如下:
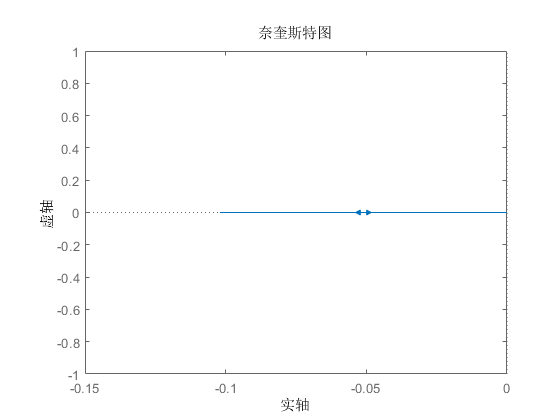
可以得到,系统没有零点,但存在两个极点,其中一个极点位于右半\(S\)平面,根据奈奎斯特稳定判据,闭环系统稳定的充分必要条件是:当\(\omega\)从\(-\infty\)到\(+\infty\)变化时,开环传递函数\(G(j\omega)\)沿逆时针方向包围\((-1,0)\)点\(p\)圈,其中\(p\)为开环传递函数在右半\(S\)平面内的极点数。对于直线一级倒立摆,由上图我们可以看出,开环传递函数在\(S\)右半平面有一个极点,因此\(G(j\omega)\)需要沿逆时针方向包围\((-1,0)\)点\(1\)圈,可以看出,系统的Nyquist图并没有逆时针绕\((-1,0)\)点\(1\)圈,因此系统不稳定,需要设计控制器来镇定系统。
超前校正的设计
稳态位置误差常数为\(10\)
相位裕量为\(50^\circ\)
增益裕量\(\ge10 \ dB\)
控制器设计步骤如下:
- 选择控制器,上面我们已经得到了系统的 Bode 图,可以看出,给系统增加一个超前校正就可以满足设计要求,设超前校正装置为:
\[ K(s)=\frac{1+\alpha Ts}{1+Ts}=\alpha\frac{\frac{1}{\alpha T}+s}{\frac{1}{T}+s} \]
已校正系统具有开环传递函数\(K_cK(s)G(s)\)
设: \[ G_1(s)=K_cG(s)=\frac{0.02725K_c}{0.0102125s^2-0.26705} \] 2. 根据稳态误差要求计算增益\(K_c\):
\[ K_p=\lim_{s\to0}K_cK(s)G(s)=\lim_{s\to0}K_c\frac{1+\alpha Ts}{1+Ts}\times\frac{0.02725}{0.0102125s^2-0.26705}=10 \]
可以得到: \[ K_c=98 \] 于是有: \[ G_1(s)=\frac{0.02725\times98}{0.0102125s^2-0.26705} \]
- 在\(MATLAB\)中画出\(G_1(s)\)的\(Bode\)图如下:
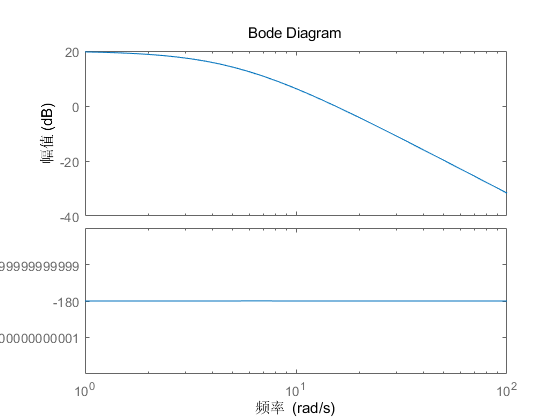
\(Nyquist\)图如下:
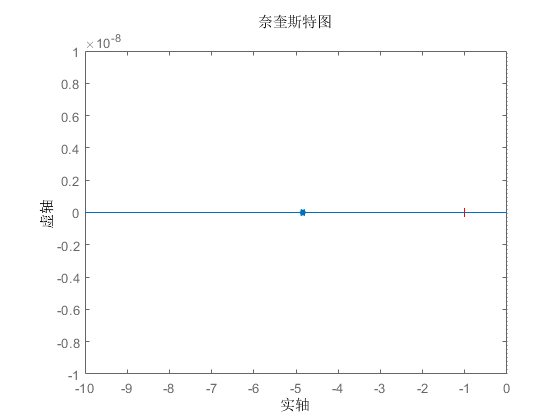
- 可以看出,系统的相位裕量为\(0^\circ\),根据设计要求,系统的相位裕量为\(50^\circ\),因此需要增加的相位裕量为\(50^\circ\),增加超前校正装置会改变Bode图的幅值曲线,这时增益交界频率会向右移动,必须对增益交界频率增加所造成的\(G_1(j\omega)\)的相位滞后增量进行补偿,因此,假设需要的最大相位超前量\(\phi_m\)近似等于\(55^\circ\)。
根据: \[ \sin\phi_m=\frac{\alpha-1}{\alpha+1} \] 计算得到:\(\alpha=10.0590\)
- 此时\(\phi_m\)所对应增加幅值为:
\[ 10\lg a=10.0256 \ dB \]
并且\(|G_1(j\omega_c)|=-10.0261 \ dB\),即: \[ |G_1(j\omega_c)|=|-\frac{0.02725\times98}{-0.0102125\omega_c^2-0.26705}|=10^{-\frac{10.0256}{20}} \] 解得:\(\omega_c=28.3409 \ rad/s\)
再根据超前校正: \[ \omega_c=\frac{1}{\sqrt{a}T} \] 解得:\(\frac{1}{T}=89.8857\),\(\frac{1}{\alpha T}=8.9359\)
- 校正装置可以确定为:
\[ \begin{align} K(s)&=\alpha\frac{\frac{1}{\alpha T}+s}{\frac{1}{T}+s}\notag \\ &=10.0590\frac{s+8.9359}{s+89.8857}\notag \end{align} \]
且\(K_c=98\)
校正后的开环传递函数为: \[ K_cK(s)G(s)=98\times10.0590\frac{s+8.9359}{s+89.8857}\times\frac{0.02725}{0.0102125s^2-0.26705} \]
增加校正后系统的\(Bode\)图如下:
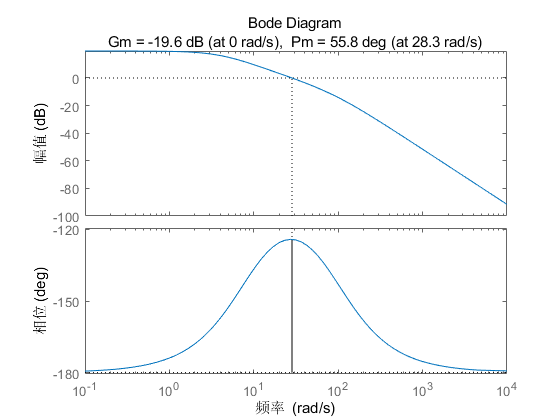
\(Nyquist\)图如下:
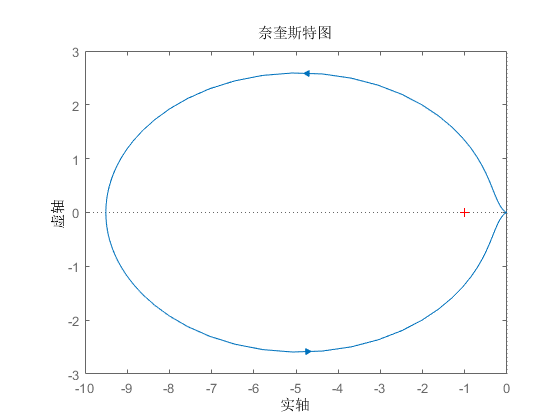
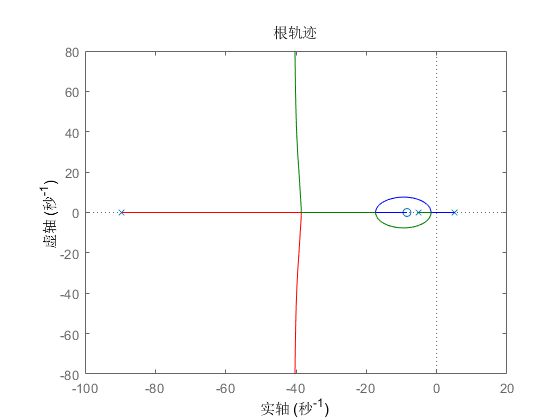
根轨迹图如下:
观察\(Bode\)图可知,校正后的相位裕度为\(55.8^\circ\),达到要求的\(50^\circ\)
系统的阶跃响应曲线如下:
系统的稳态值为\(1.12\),稳态误差大于\(0.1\),未满足题设要求,超调量\(\sigma\%=13.39\%\),调节时间\(t_s=0.324s\)。
系统的冲激响应曲线如下:
可以看到,系统在遇到干扰后,可以在\(0.4s\)内达到新的平衡,但是震荡幅度较大。
滞后-超前校正的设计
超前校正虽然使得系统迅速达到了平衡,但存在稳态误差,同时震荡幅度较大,因此需要引入滞后校正来改善系统响应,使得在稳态精度、快速性和震荡性达到较好的平衡。
控制器设计步骤如下:
- 设滞后-超前校正装置为:
\[ K(s)=\frac{(1+T_bs)(1+T_as)}{(1+\alpha T_bs)(1+\alpha^{-1}T_as)} \]
已校正系统具有开环传递函数\(K_cG(s)K(s)\)
- 根据稳态误差要求计算增益\(K_c\),为减小稳态误差,故选取更大的稳态位置误差常数\(K_p\):
\[ K_p=\lim_{s\to0}K_cK(s)G(s)=\lim_{s\to0}K_c\frac{(1+T_bs)(1+T_as)}{(1+\alpha T_bs)(1+\alpha^{-1}T_as)}\times\frac{0.02725}{0.0102125s^2-0.26705}=100 \]
可以得到: \[ K_c=980 \]
- 根据:
\[ \sin\phi_m=\frac{\alpha-1}{\alpha+1} \]
取\(\phi_m=55^\circ\),计算得到:\(\alpha=10.0590\)
- 根据取截止频率\(\omega_c=28 \ rad/s\),并且设\(T_a=0.1107\),有:
\[ 20\lg K_c+20\lg|G(j\omega_c)|+20\lg|\frac{1+T_bj\omega_c}{1+\alpha T_bj\omega_c}|+20\lg|\frac{1+T_a j\omega_c}{1+\alpha^{-1} T_aj\omega_c}|=0 \]
解得:\(T_b=0.7054\)
- 最终滞后-超前控制器为:
\[ K(s)=\frac{(0.7054s+1)(0.1107s+1)}{(7.0956s+1)(1.1005\times10^{-2} s+1)} \] 且\(K_c=980\)
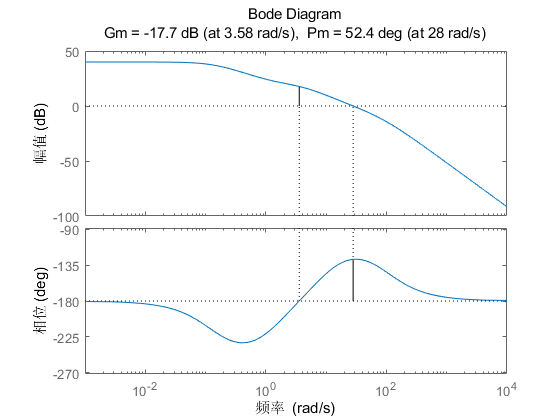
校正后的开环传递函数为: \[ K_cK(s)G(s)=980\times\frac{(0.7054s+1)(0.1107s+1)}{(7.0956s+1)(1.1005\times10^{-2} s+1)}\times\frac{0.02725}{0.0102125s^2-0.26705} \] 增加校正后系统的\(Bode\)图如下:
\(Nyquist\)图如下:
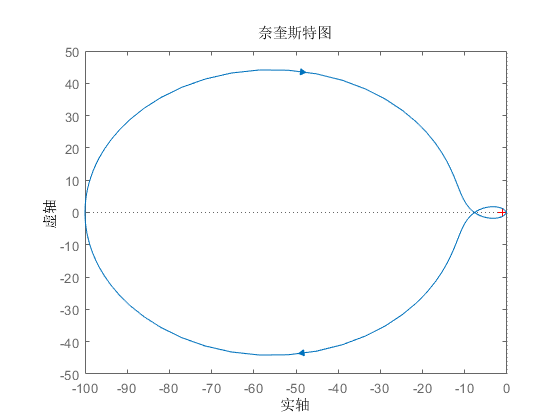
根轨迹图如下:
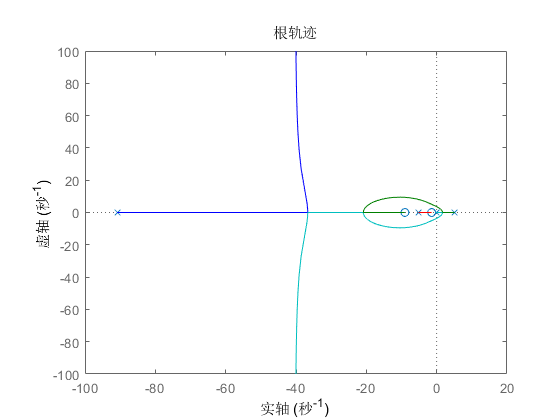
观察\(Bode\)图可知,校正后的相位裕度为\(52.4^\circ\),达到要求的\(50^\circ\),增益裕量为\(17.7dB\),达到要求的\(10dB\)
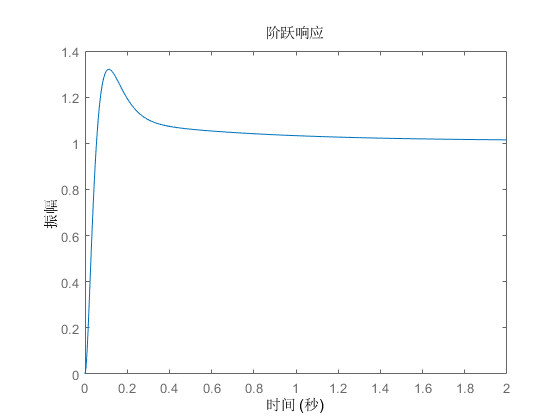
系统的阶跃响应曲线如下:
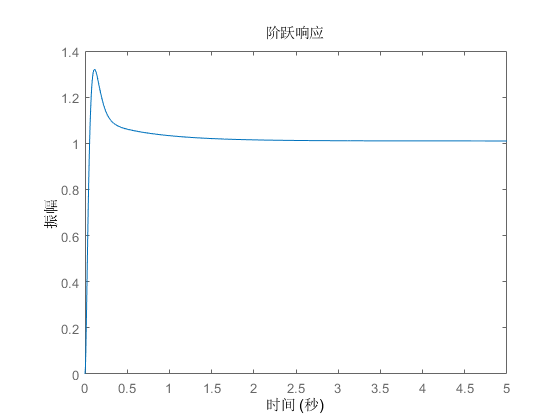
系统的稳态值为\(1.01\),稳态误差小于\(0.1\),满足题设要求,超调量\(\sigma\%=30.69\%\),调节时间\(t_s=0.96s\)。
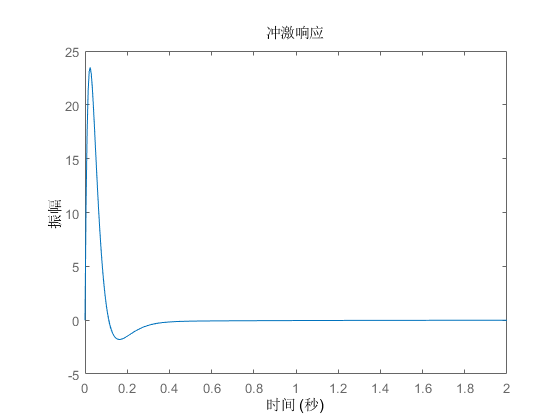
系统的冲激响应曲线如下:
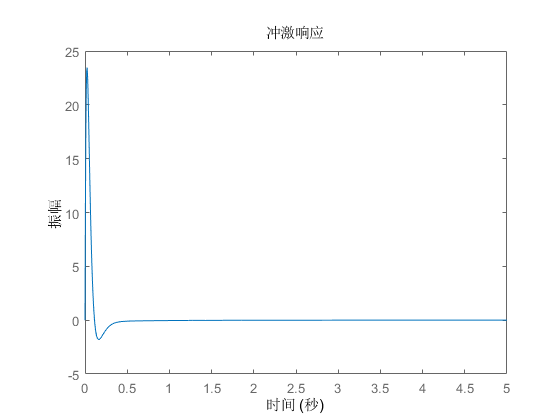
可以看到,系统在遇到干扰后,可以在\(0.4s\)内达到新的平衡,但是振荡幅度较大。










