对于倒立摆系统,由于其本身是自不稳定的系统,实验建模存在一定的困难。但是忽略掉一些次要的因素后,倒立摆系统就是一个典型的运动的刚体系统,可以在惯性坐标系内应用经典力学理论建立系统的动力学方程。
倒立摆系统的建模
可将倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示
其中
\(M\):小车质量
\(m\):摆杆质量
\(b\):小车摩擦系数
\(l\):摆杆转动轴心到杆质心的长度(当杆均匀时,长度为\(2l\))
\(I\):摆杆转动惯量
\(F\):加在小车上的力
\(x\):小车位置
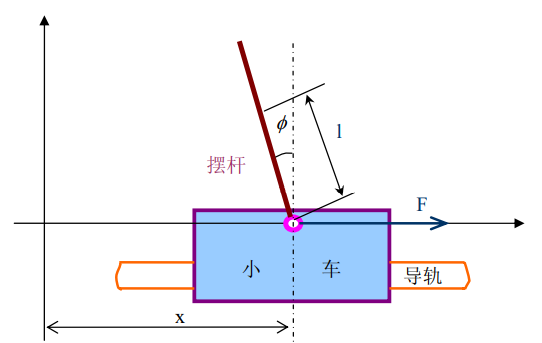
其中\(\phi\)为摆杆与垂直向上方向的夹角,\(\theta\)为摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下),有\(\theta=\phi+\pi\)。
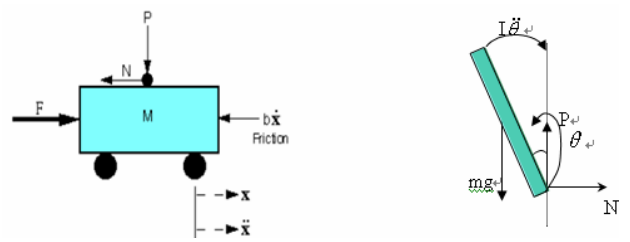
分析小车水平方向所受的合力,可以得到以下方程: \[ M\ddot x=F-b\dot x-N \tag{1} \] 由摆杆水平方向所受的合力,可以得到以下方程: \[ \begin{align} N&=m\frac{d^2}{dt^2}(x+l\sin\theta)\notag \\ &=m\ddot x+ml\frac{d}{dt}(\dot\theta\cos\theta)\notag \\ &=m\ddot x+ml\ddot\theta\cos\theta-ml\dot\theta^2\sin\theta\tag{2} \end{align} \] 合并(1)(2)得: \[ (M+m)\ddot x+b\dot x+ml(\ddot\theta\cos\theta-ml\dot\theta^2\sin\theta)=F\tag{3} \] 对摆杆垂直方向上的合力进行分析,可以得到以下方程: \[ \begin{align} P-mg&=-m\frac{d^2}{dt^2}(l\cos\theta)\notag \\ &=ml\frac{d}{dt}(\dot\theta\sin\theta)\notag \\ &=ml\ddot\theta\sin\theta+ml\dot\theta^2\cos\theta\tag{4} \end{align} \] 力矩平衡方程如下: \[ \begin{align} Pl\sin\phi+Nl\cos\phi&=I\ddot\theta\notag \\ -Pl\sin\theta-Nl\cos\theta&=I\ddot\theta\tag{5} \end{align} \] 联立(2)(4)(5),消去\(N\)和\(P\)得: \[ (I+ml^2)\ddot\theta+mgl\sin\theta=-ml\ddot x\cos\theta\tag{6} \] 根据\(\phi\)和\(\theta\)定义知\(\theta=\phi+\pi\),当摆杆处于竖直位置时,\(\phi\)接近于\(0\),则有\(\cos\theta=-\cos\phi\approx-1\),\(\sin\theta=-\sin\phi\approx-\phi\),\(\dot\theta^2\approx0\),\(\ddot\theta=\ddot\phi\)并使用\(u\)来代表输入力\(F\),代入到(3)(6),得线性化运动方程如下: \[ \begin{cases} (M+m)\ddot x+b\dot x-ml\ddot\phi=u \\ (I+ml^2)\ddot\phi-mgl\phi=ml\ddot x \end{cases}\tag{7} \]
建立系统的状态空间模型
求解(7),可得: \[ \begin{cases} \dot x=\dot x \\ \ddot x=-\frac{(I+ml^2)b}{p}\dot x+\frac{m^2gl^2}{p}\phi+\frac{I+ml^2}{p}u \\ \dot\phi=\dot\phi \\ \ddot\phi=-\frac{mbl}{p}\dot x+\frac{mgl(M+m)}{p}\phi+\frac{ml}{p}u \end{cases}\tag{8} \] 整理后得到系统状态空间方程: \[ \begin{bmatrix} \dot x \\ \ddot x \\ \dot\phi \\ \ddot\phi \\ \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & -\frac{(I+ml^2)b}{p} & \frac{m^2gl^2}{p} & 0 \\ 0 & 0 & 0 & 1\\ 0 & -\frac{mbl}{p} & \frac{mgl(M+m)}{p} & 0\\ \end{bmatrix} \begin{bmatrix} x \\ \dot x \\ \phi \\ \dot\phi \\ \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{I+ml^2}{p} \\ 0 \\ \frac{ml}{p} \\ \end{bmatrix} u\tag{9} \] 输出方程如下: \[ y= \begin{bmatrix} x \\ \phi \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot x \\ \phi \\ \dot\phi \\ \end{bmatrix}\tag{10} \]
其中\(p=(M+m)I+Mml^2\)
建立系统简化的状态空间模型
在理想情况下,摆杆转动惯量\(I=\frac{1}{3}ml^2\),摩擦系数\(b=0\),小车质量\(M\)远大于摆杆质量\(m\),即\(M\gg m\),代入到(9)(10)得到理想情况下的系统状态空间方程: \[ \begin{bmatrix} \dot x \\ \ddot x \\ \dot\phi \\ \ddot\phi \\ \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1\\ 0 & 0 & \frac{3g}{4l} & 0\\ \end{bmatrix} \begin{bmatrix} x \\ \dot x \\ \phi \\ \dot\phi \\ \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 0 \\ \frac{3}{4l} \\ \end{bmatrix} u\tag{11} \] 理想情况下的系统输出方程: \[ y= \begin{bmatrix} x \\ \phi \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ \dot x \\ \phi \\ \dot\phi \\ \end{bmatrix}\tag{12} \]
建立系统传递函数模型
对(7)进行拉普拉斯变换得: \[ \begin{cases} (M+m)X(s)s^2+bX(s)s-ml\Phi(s)s^2=U(s) \\ (I+ml^2)\Phi(s)s^2-mgl\Phi(s)=mlX(s)s^2 \end{cases}\tag{13} \] 注:推导传递函数时假设初始条件为\(0\)。
整理(13)的第二个方程得: \[ \frac{\Phi(s)}{X(s)}=\frac{mls^2}{(I+ml^2)s^2-mgl}\tag{14} \] 如果令\(v=\ddot x\),则有: \[ \frac{\Phi(s)}{V(s)}=\frac{ml}{(I+ml^2)s^2-mgl}\tag{15} \]
将(14)代入(13)的第一个方程消去\(X(s)\),整理得: \[ \frac{\Phi(s)}{U(s)}=\frac{\frac{ml}{q}s}{s^3+\frac{b(I+ml^2)}{q}s^2-\frac{(M+m)mgl}{q}s-\frac{bmgl}{q}}\tag{16} \] 将(16)代入(14)消去\(\Phi(s)\),整理得: \[ \frac{X(s)}{U(s)}=\frac{\frac{I+ml^2}{q}s^2-\frac{mgl}{q}}{s^4+\frac{b(I+ml^2)}{q}s^3-\frac{(M+m)mgl}{q}s^2-\frac{bmgl}{q}s}\tag{17} \] 其中\(q=(M+m)(I+ml^2)-m^2l^2\)
系统可控性分析
状态空间模型
\[ A= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & -\frac{(I+ml^2)b}{p} & \frac{m^2gl^2}{p} & 0 \\ 0 & 0 & 0 & 1\\ 0 & -\frac{mbl}{p} & \frac{mgl(M+m)}{p} & 0\\ \end{bmatrix} , B= \begin{bmatrix} 0 \\ \frac{I+ml^2}{p} \\ 0 \\ \frac{ml}{p} \\ \end{bmatrix} , C= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \]
其中\(p=(M+m)I+Mml^2\)
将实际参数:
- \(M=1.096kg\)
- \(m=0.109kg\)
- \(b=0.1N\cdot s/m\)
- \(l=0.25m\)
- \(I=0.0034kg\cdot m^2\)
代入得: \[ A= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & -0.0883 & 0.6293 & 0 \\ 0 & 0 & 0 & 1\\ 0 & -0.2357 & 27.8285 & 0\\ \end{bmatrix} , B= \begin{bmatrix} 0 \\ 0.8832 \\ 0 \\ 2.3566 \\ \end{bmatrix} , C= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \] 计算得到可控性矩阵: \[ S_1= \begin{bmatrix} 0 & 0.8832 & -0.0780 & 1.4899 \\ 0.8832 & -0.0780 & 1.4899 & -0.2626 \\ 0 & 2.3566 & -0.2081 & 65.5978\\ 2.3566 & -0.2081 & 65.5978 & -6.1429\\ \end{bmatrix} \] 并且有\(rank(S_1)=4\),故该系统完全可控。
计算得到可观测性矩阵: \[ V_1= \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & -0.0883 & 0.6293 & 0\\ 0 & -0.2357 & 27.8285 & 0\\ 0 & 0.0078 & -0.0556 & 0.6293\\ 0 & 0.0208 & -0.1483 & 27.8285 \end{bmatrix} \] 并且有\(rank(V_1)=4\),故该系统完全可观测。
\(MATLAB\)代码如下:
1 | M=1.096;m=0.109;b=0.1;l=0.25;I=0.0034;g=9.8; |
简化的状态空间模型
\[ A= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1\\ 0 & 0 & \frac{3g}{4l} & 0\\ \end{bmatrix} , B= \begin{bmatrix} 0 \\ 1 \\ 0 \\ \frac{3}{4l} \\ \end{bmatrix} , C= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \]
将实际参数代入得: \[ A= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1\\ 0 & 0 & 29.4 & 0\\ \end{bmatrix} , B= \begin{bmatrix} 0 \\ 1 \\ 0 \\ 3 \\ \end{bmatrix} , C= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \] 计算得到可控性矩阵: \[ S_2= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 3 & 0 & 88.2\\ 3 & 0 & 88.2 & 0\\ \end{bmatrix} \] 并且有\(rank(S_2)=4\),故该系统完全可控。
计算得到可观测性矩阵: \[ V_1= \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 29.4 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 29.4 \end{bmatrix} \] 并且有\(rank(V_2)=4\),故该系统完全可观测。
\(MATLAB\)代码如下:
1 | M=1.096;m=0.109;b=0.1;l=0.25;I=0.0034;g=9.8; |
开环系统在典型信号作用下的响应
系统的状态空间模型
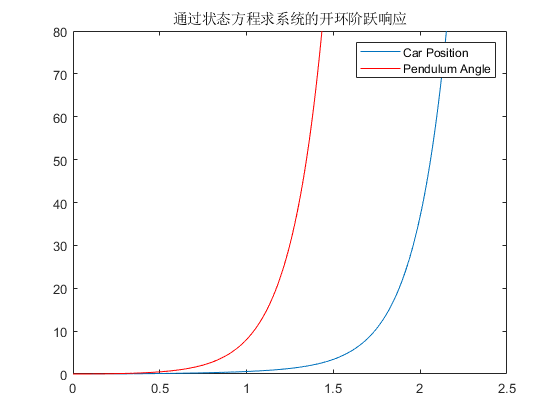
单位阶跃响应
系统的单位阶跃响应如下图所示:
\(MATLAB\)代码如下:
1 | M=1.096;m=0.109;b=0.1;l=0.25;I=0.0034;g=9.8;T=0.001; |
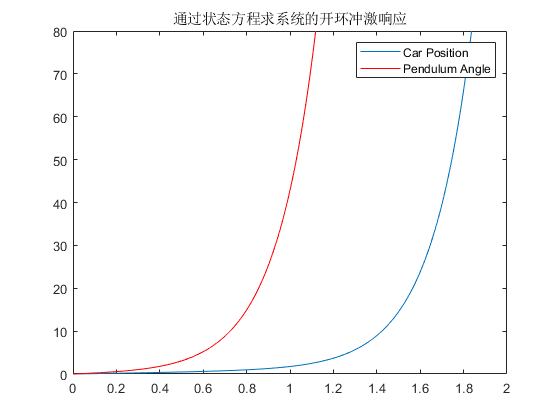
单位冲激响应
系统的单位冲激响应如下图所示:
\(MATLAB\)代码如下:
1 | M=1.096;m=0.109;b=0.1;l=0.25;I=0.0034;g=9.8; |
系统简化的状态空间模型
单位阶跃响应
系统的单位阶跃响应如下图所示:
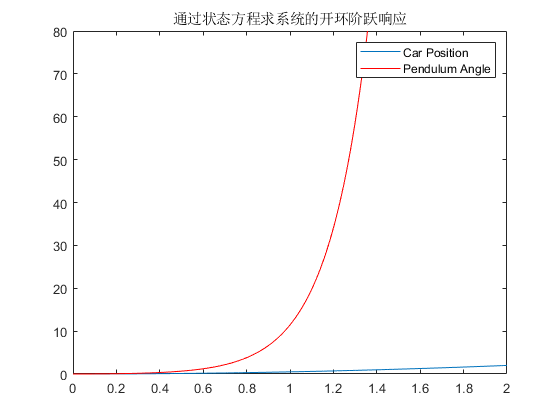
\(MATLAB\)代码如下:
1 | l=0.25;g=9.8;T=0.001; |
单位冲激响应
系统的单位冲激响应如下图所示:
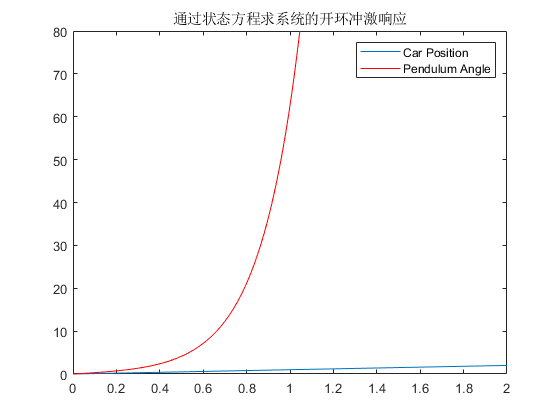
\(MATLAB\)代码如下:
1 | l=0.25;g=9.8;T=0.001; |
系统的传递函数模型
单位阶跃响应
系统的单位阶跃响应如下图所示:
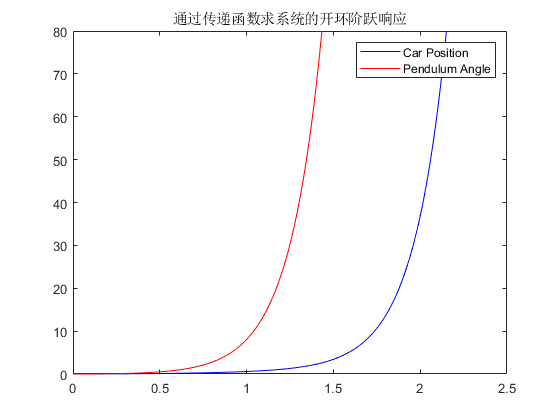
\(MATLAB\)代码如下:
1 | M=1.096;m=0.109;b=0.1;l=0.25;I=0.0034;g=9.8;T=0.001; |
单位冲激响应
系统的单位冲激响应如下图所示:
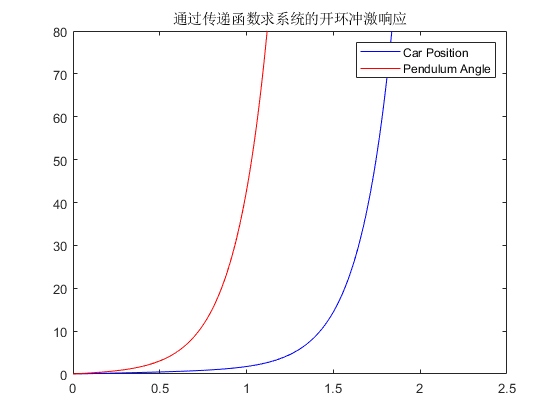
\(MATLAB\)代码如下:
1 | M=1.096;m=0.109;b=0.1;l=0.25;I=0.0034;g=9.8;T=0.001; |
结论
通过对系统进行建模并进行理论分析和仿真可知,倒立摆系统在开环状态下不稳定,无法自行平衡,因此需要设计合适的控制器来对倒立摆系统进行控制,以达到期望的稳定控制效果。










