经典控制理论的研究对象主要是单输入单输出的系统,控制器设计时一般需要有关被控对象的较精确模型。PID 控制器因其结构简单,容易调节,且不需要对系统建立精确的模型,在控制上应用较广。
经典控制理论的研究对象主要是单输入单输出的系统,控制器设计时一般需要有关被控对象的较精确模型,现代控制理论主要是依据现代数学工具,将经典控制理论的概念扩展到多输入多输出系统。极点配置法通过设计状态反馈控制器将多变量系统的闭环系统极点配置在期望的位置上,从而使系统满足瞬态和稳态性能指标。
PID和极点配置实验
直线一级倒立摆 PID 控制实验
PID控制器原理
PID控制器的传递函数为: \[ KD(s)=K_Ds+Kp+\frac{K_I}{s}=\frac{K_Ds^2+K_Ps+K_I}{s} \] 通过分析PID控制器的传递函数与被控对象的传递函数,就可以得到系统的各项性能指标。
在实际当中,需要仔细调节PID控制器的参数,以便达到满意的控制效果。
PID 控制参数设定及仿真
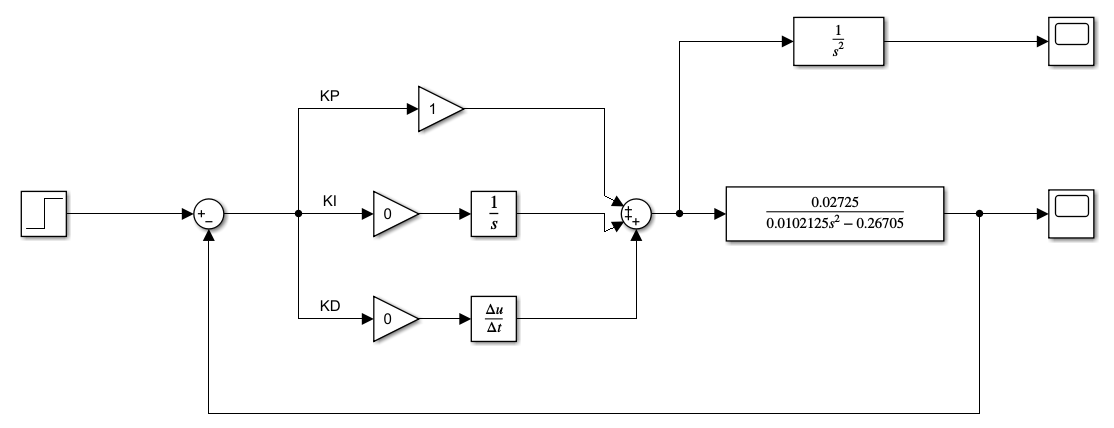
在\(Simulink\)中搭建如下模型:
此时相当于无控制器,阶跃响应曲线不收敛。
逐渐增大控制量\(K_P=40\),系统由发散逐步转为等幅振荡,增大\(K_P\),震荡频率增加,同时震荡幅度减小。
\(K_P=40,K_I=0,K_D=0\)时的阶跃响应曲线如下图所示:
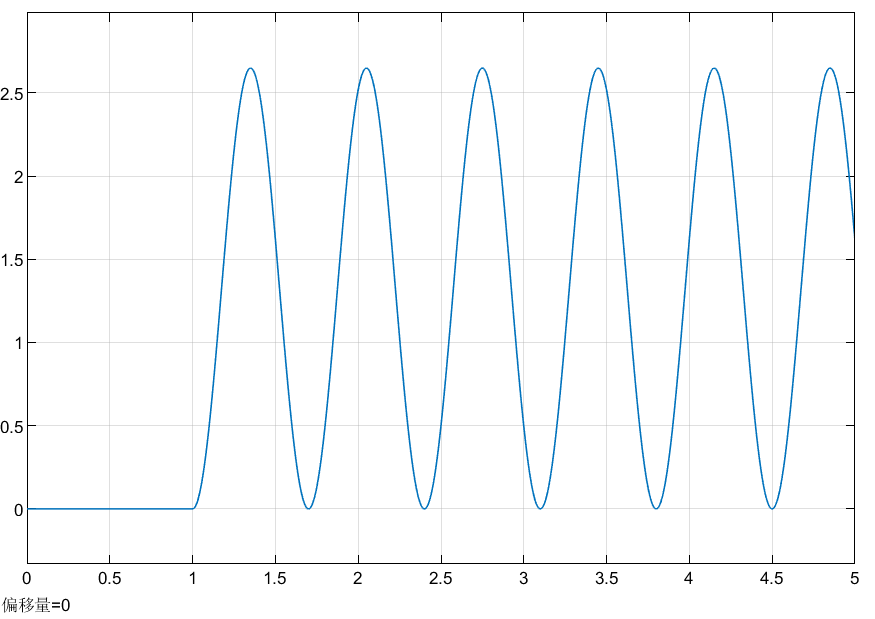
逐步增大控制量\(K_D\),系统震荡逐步减小,同时到稳定时所经历的震荡周期个数减小。\(K_D\)过小时,系统震荡较为严重,达到稳态的时间较长;\(K_D\)过大时,系统震荡减缓,但上升时间变慢,达到稳态的时间同样会加长。最终选定\(K_D=5.7\),上升速度足够快的同时,震荡极小,调节时间也令人满意。
\(K_P=40,K_I=0,K_D=5.7\)时的阶跃响应曲线如下图所示:
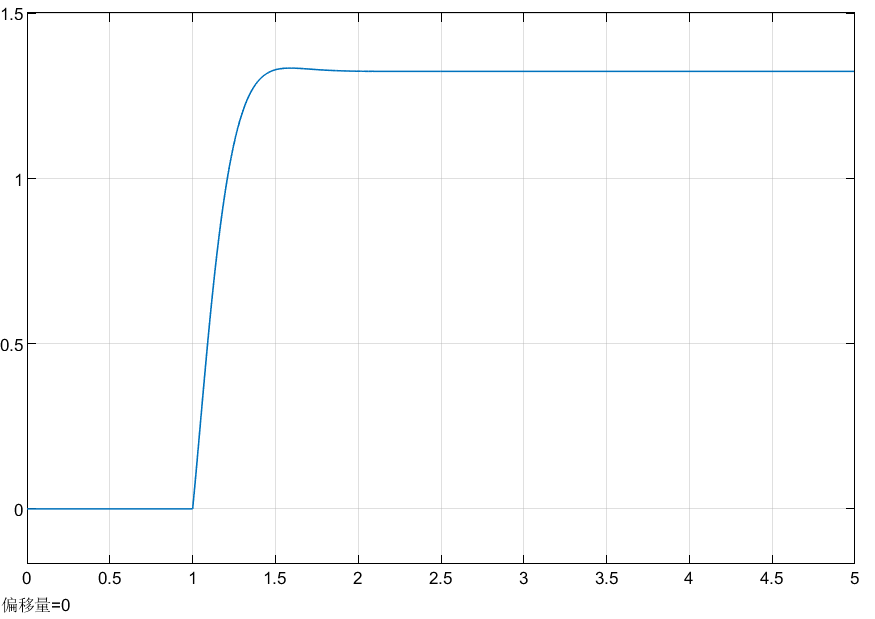
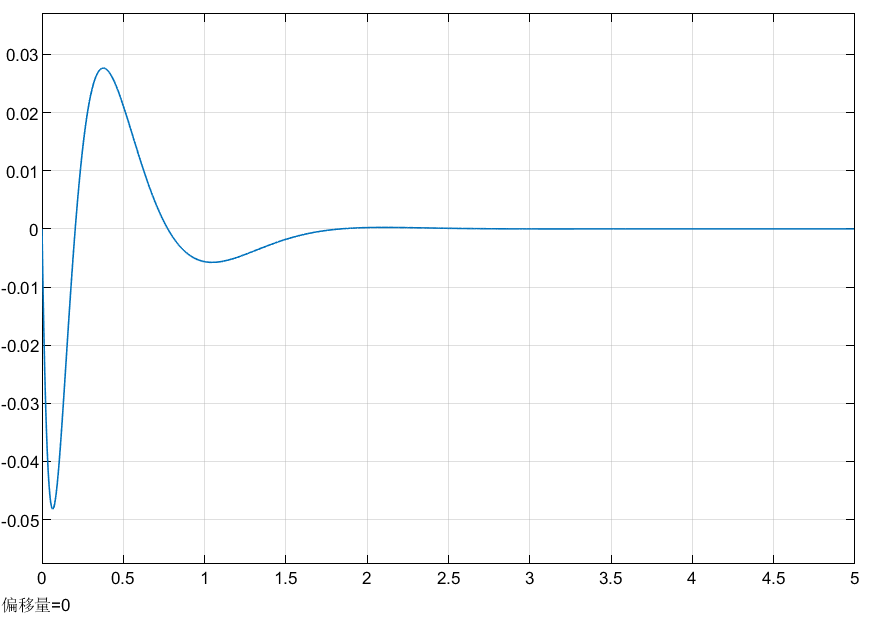
为了最终消除稳态误差,需要引入积分控制。
逐渐增大控制量\(K_I\),稳态误差趋于\(0\)的速度也逐渐增加,但随着\(K_I\)的增大,系统的超调量也逐渐增大,因此最终选定\(K_I=40\),此时稳态误差几乎为\(0\),调节时间\(t_s=2.133s(2\%)\),超调量\(\sigma\%=40.9%\)。
\(K_P=40,K_I=40,K_D=5.7\)时的阶跃响应曲线如下图所示:
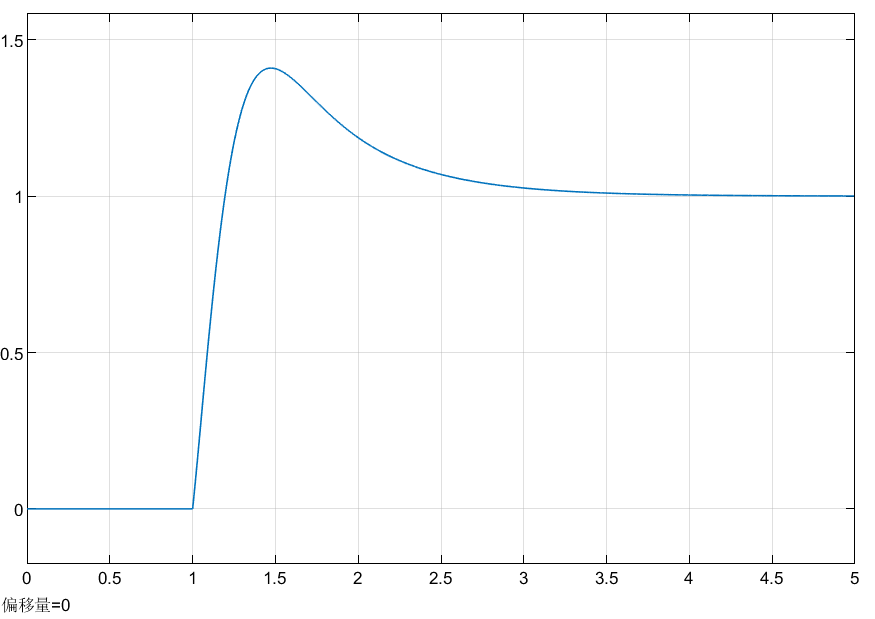
此时观察小车位置的变化曲线如下:
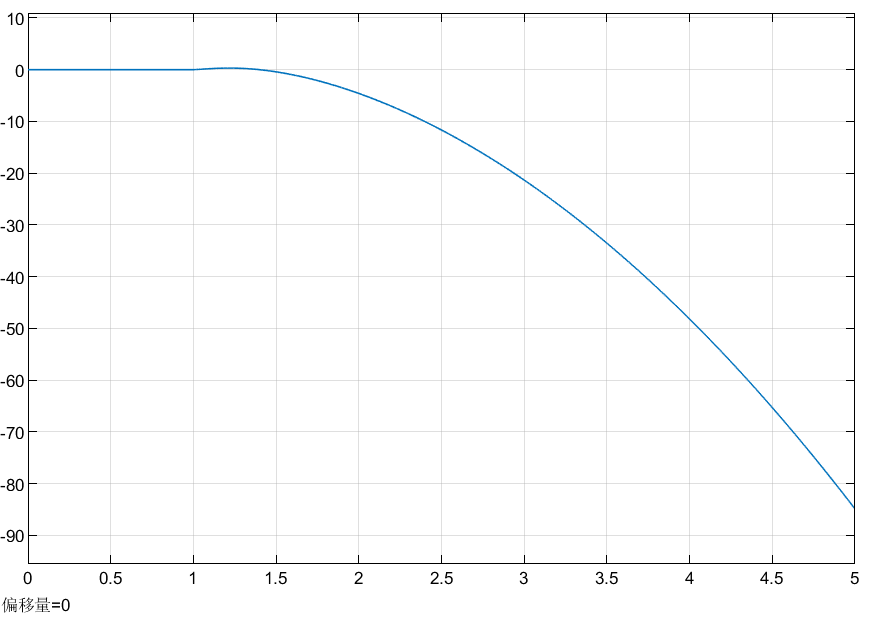
可以看出,由于PID控制器为单输入单输出系统,所以只能控制摆杆的角度,并不能控制小车的位置,所以小车会往一个方向运动。
状态空间极点配置控制实验
经典控制理论的研究对象主要是单输入单输出的系统,控制器设计时一般需要有关被控对象的较精确模型,现代控制理论主要是依据现代数学工具,将经典控制理论的概念扩展到多输入多输出系统,即建立系统的状态空间表达。极点配置法通过设计状态反馈控制器将多变量系统的闭环系统极点配置在期望的位置上,从而使系统满足瞬态和稳态性能指标。前面我们已经得到了倒立摆系统的比较精确的动力学模型,下面我们针对直线型一级倒立摆系统应用极点配置法设计控制器。
状态空间分析
对于控制系统: \[ \dot x=Ax+Bu \] 式中
- \(x\)为状态向量(\(n\)维列向量)
- \(u\)为控制向量(纯量)
- \(A\)为\(n\times n\)维常数矩阵
- \(B\)为\(n\times1\)维常数矩阵
选择控制信号为: \[ u=-Kx \] 求解得: \[ \dot x=(A-BK)x \] 方程的时域解为: \[ x(t)=e^{(A-BK)t}x(0) \] 可以看出,如果系统状态完全可控,\(K\)选择适当,对于任意的初始状态,当\(t\)趋于无穷时,都可以使\(x(t)\)趋于\(0\)。
极点配置设计步骤
方法一:
- 检验系统可控性。
- 计算特征值:根据根据要求,并留有一定的裕量(设调整时间为 2 秒),取阻尼比为最佳阻尼比即\(\zeta=\frac{\sqrt 2}{2}\approx0.707107\)。
再由调节时间: \[ t_s=\frac{4}{\zeta\omega_n}\le2 \ (2\%) \] 解得固有频率\(\omega_n\ge2.8284rad/s\),取固有频率\(\omega_n=3\sqrt{2} \ rad/s\)。
则期望闭环极点为\(\lambda_1=-3+3j,\lambda_2=-3-3j\),另外两个闭环极点位于\(\lambda_1\)和\(\lambda_2\)的左边,且距离虚轴更远,因此\(\lambda_1\)和\(\lambda_2\)作为主导闭环极点,其余闭环极点对系统响应影响较小,可取\(\lambda_3=-10,\lambda_4=-10\),因此期望的特征方程为: \[ \begin{align} (s-\lambda_1)(s-\lambda_2)(s-\lambda_3)(s-\lambda_4)&=(s+3-3j)(s+3+3j)(s+10)(s+10)\notag \\ &=s^4+26s^3+283s^2+960s+1800\notag \end{align} \] 因此可得: \[ \beta_1=26,\beta_2=283,\beta_3=960,\beta_4=1800 \] 由系统特征方程: \[ \begin{align} |sI-A|&= \left |\begin{array}{} s & -1 & 0 & 0 \\ 0 & s & 0 & 0 \\ 0 & 0 & s & -1 \\ 0 & 0 & -29.4 & s \end{array}\right|\notag \\ &=s^4-29.4s^2\notag \end{align} \] 因此可得: \[ \alpha_1=0,\alpha_2=-29.2,\alpha_3=0,\alpha_4=0 \] 系统的反馈增益阵为: \[ K= \begin{bmatrix} \beta_4-\alpha_4 & \beta_3-\alpha_3 & \beta_2-\alpha_2 & \beta_1-\alpha_1 \end{bmatrix} \times P \]
- 确定使状态方程变为可控标准型的变换矩阵\(P\)
\[ P= \begin{bmatrix} -0.034 & 0 & 0.0113 & 0 \\ 0 & -0.034 & 0 & 0.0113 \\ 0 & 0 & 0.3333 & 0 \\ 0 & 0 & 0 & 0.3333 \end{bmatrix} \]
- 状态反馈增益矩阵\(K\)为:
\[ \begin{align} K&= \begin{bmatrix} \beta_4-\alpha_4 & \beta_3-\alpha_3 & \beta_2-\alpha_2 & \beta_1-\alpha_1 \end{bmatrix} \times P\notag \\ &= \begin{bmatrix} 1800 & 960 & 312.4 & 26 \end{bmatrix} \times \begin{bmatrix} -0.034 & 0 & 0.0113 & 0 \\ 0 & -0.034 & 0 & 0.0113 \\ 0 & 0 & 0.3333 & 0 \\ 0 & 0 & 0 & 0.3333 \end{bmatrix}\notag \\ &= \begin{bmatrix} -61.2245& -32.6531 & 109.5415 & 19.5510 \end{bmatrix}\notag \end{align} \]
方法二:
设反馈增益矩阵\(K\)为: \[ K=\begin{bmatrix} k_1 & k_2 & k_3 & k_4 \end{bmatrix} \] 矩阵\((A-BK)\)的特征值是方程式\(|sI-(A-BK)|=0\)的根:
即特征的多项式: \[ s^4+(k_2+3k_4)s^3+(-29.4+k_1+3k_3)s^2-29.4k_2s-29.4k_1=0 \] 与期望特征多项式比较: \[ s^4+26s^3+283s^2+960s+1800=0 \] 使得对应项系数相同,可以列方程组,并通过解方程组也可以求出反馈增益矩阵\(K\),最终结果与方法一求解相同。
位置\(x\)响应曲线如下图所示:
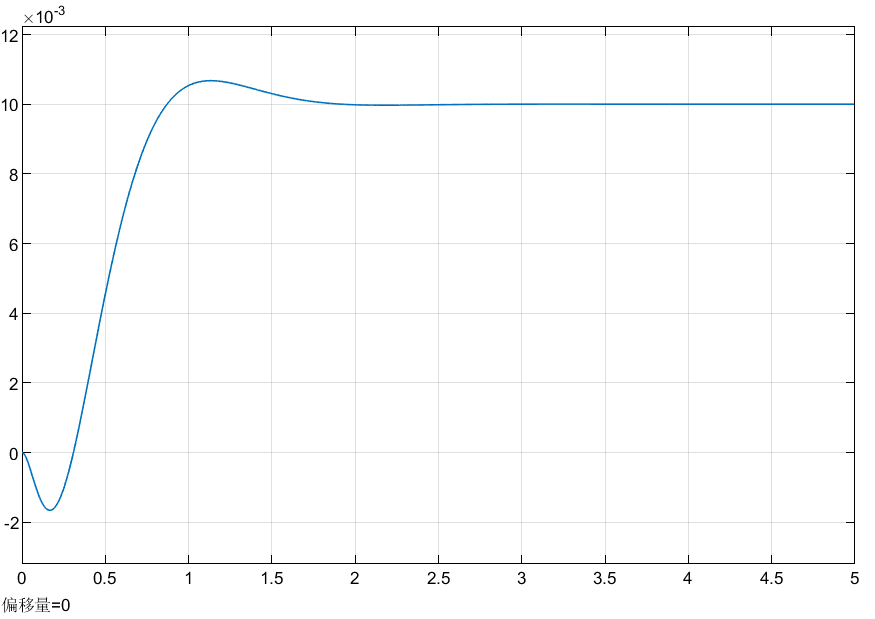
加速度\(\dot x\)响应曲线如下图所示:
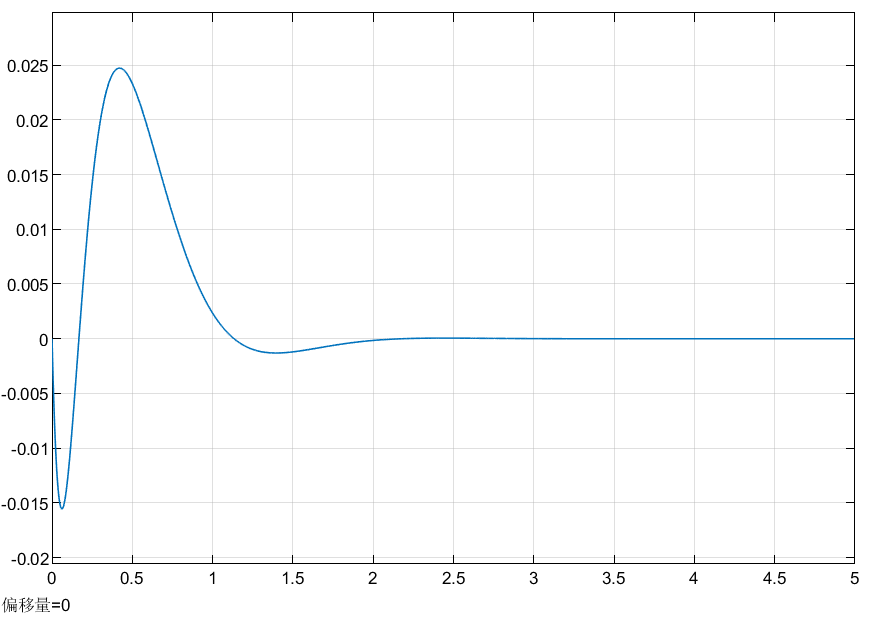
摆角\(\phi\)响应曲线如下图所示:
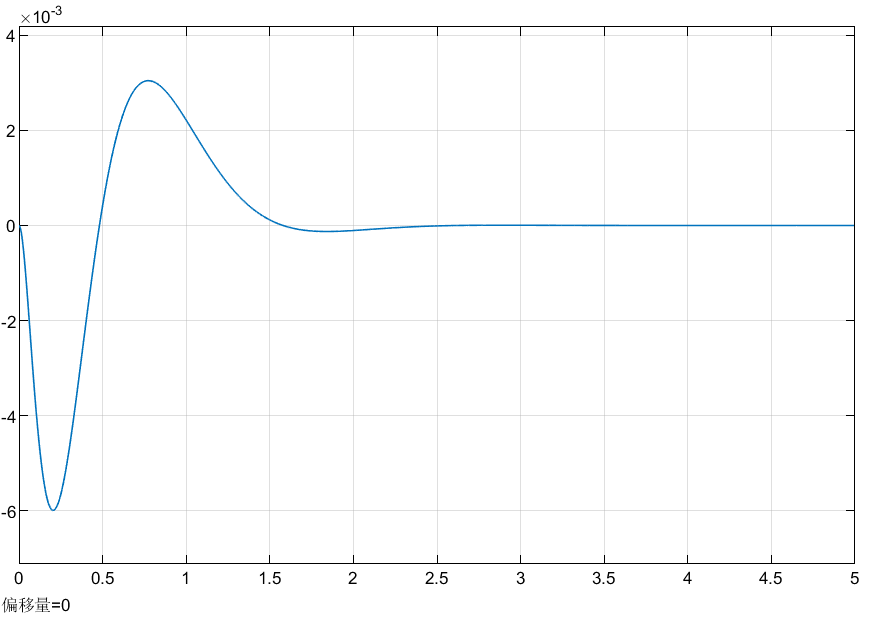
摆角加速度\(\dot\phi\)响应曲线如下图所示: